Az előadáson ebben a félévben gyűrűkről, kódelméletről, lineáris algebráról, és ha az idő engedi, akkor némi hálóelméletről lesz szó. Elsősorban a gyűrűelméletben továbbra is arra fogunk törekedni, hogy mélyebb elméleteket, eszközöket megismerjünk, és alkalmazzuk őket látszólag elemi problémák megoldására. Ezért az anyag követése továbbra is folyamatos erőfeszítést igényel, minden második órára nem érdemes beülni.
Az írásbeli házi feladatokra a kitűzést követő két héten belül kérem a választ. Aki ily módon a lehetséges pontszám 80 százalékát megszerzi az jeles, 65 százalékra jó, 50 százalékra közepes osztályzatot kap a félév végi vizsgajegyként. Aki ezzel a lehetőséggel nem kíván élni, az a félév végén szóbeli vizsgát tehet, amin az összes elhangzott tételt és bizonyítást tudni és érteni kell.
1. alkalom. Weddernburn tételének bizonyítása (minden véges test kommutatív). A modulus fogalma, példák.
Írásban beadható házi feladat: Bizonyítsuk be, hogy ha K kommutatív test, és G véges részcsoportja K multiplikatív csoportjának, akkor G ciklikus.
2. alkalom. Gyűrűk Jacobson-radikálja: példák. Egyszerű modulus, Schur-lemma, sűrűségi tétel.
Írásban beadható házi feladat: Legyen D ferdetest, V egy n-dimenziós vektortér D felett, és R a V vektortér D-lineáris transzformációinak gyűrűje. Tegyük V-t R-modulussá úgy, hogy az összeadás a V-beli vektortér-összeadás, és ha A egy R-beli lineáris transzformáció, akkor az Av modulus-szorzat értéke A(v). Számítsuk ki az ebből a modulusból a Schur-lemma által származtatott ferdetestet.
3. alkalom. A Jacobson radikál definíciója mint az összes egyszerű modulust annulláló elemek halmaza. A kör-művelet, és a kvázi-inverz fogalma. A Jacobson-radikál jellemzése.
Írásban beadható házi feladat: Számítsuk ki az alábbi gyűrűk Jacobson-radikálját: Z36; a páratlan nevezőjű (racionális) törtek; a 2-hatvány nevezőjű (racionális) törtek; C[x]/(x6) (ahol C a komplex számok teste).
4. alkalom. A Jacobson-radikál szerinti faktor sűrű mátrixgyűrűk szubdirekt szorzata. Derivációk. A kommutativitási tétel bizonyítása.
5. alkalom. Artin-gyűrűk radikálja nilpotens, a szerinte vett faktor teljes mátrixgyűrűk direkt szorzata. A Zorn-lemma és alkalmazásai: minden vektortérnek van bázisa; minden egységelemes gyűrűnek van maximális ideálja.
Írásban beadható házi feladat: Mutassuk meg, hogy egy véges gyűrű akkor és csak akkor testek direkt szorzata, ha nincs olyan nem nulla eleme, aminek a négyzete nulla.
6. alkalom. A König-lemma. Ultrafilter konstukciója a Zorn-lemma segítségével. A végtelen Ramsey-tétel. Sierpinski példája. Ha egy gráf minden véges részgráfja szinezhető k színnel, akkor a gráf maga is.
Írásban beadható házi feladat: Mutassuk meg, hogy minden végesen generált csoportnak van maximális részcsoportja.
7. alkalom. A kódelmélet alapjai. BCH kódok (lásd Freud: Lineáris algebra).
Írásban beadható házi feladat: Adjuk meg a 64 elemű test feletti 2-hibajavító BCH-kód paritásellenőrző mátrixát. (Nem kell minden elemet kiszámolni, csak azt kell leírni, hogy konkrétan mi lesz a testnek primitív eleme, és ebből hogyan számíthatók a mátrix elemei.)
8. alkalom. Egyforma területű sokszögek a síkon egymásba átdarabolhatók. A kocka és a vele egyenlő térfogatú szabályos tetraéder nem darabolhatók át egymásba (lásd Freud: Lineáris algebra).
9. alkalom. Bilineáris függvény és kvadratikus alak valós felett, kapcsolatuk. Minden szimmetrikus bilineáris függvény diagonalizálható. (Lásd Freud: Lineáris algebra.)
10. alkalom. Kvadratikus alak jellege, a jelleg megállapítása aldeterminánsokkal. Sylvester tehetetlenségi tétele. Bilineáris függvények komplex felett. Ermitikus bilineáris függvény, kvadratikus alakok.
Írásban beadható házi feladat: Adjuk meg az y=x2 parabolához tartozó kvadratikus alakot, transzformáljuk négyzetösszeggé, és adjuk meg a jellegét.
11. alkalom. Euklideszi tér, merőlegesség, hossz. Az adjungált transzformáció. Normális, unitér, önadjungált, ortogonális, szimmetrikus transzformációk. Komplex feletti normális transzformáció ortonormált bázisban diagonalizálható.
Írásban beadható házi feladat: Transzformáljuk ortonormált bázisban négyzetösszeggé az
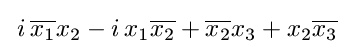
(komplex térbeli) kvadratikus alakot.
12. alkalom. Valós felett pontosan a szimmetrikus transzformációk diagonalizálhatók ONB-ben. A főtengelytétel. A sajátvektorok extremális tulajdonsága. Minden távolságtartó transzformáció ortogonális forgatásokból és tükrözésekből rakható össze.
Részben rendezett halmazok és hálók. Teljes hálók. A dualitás elve.
13. alkalom. Disztributív hálók, Stone reprezentációs tétele. Hálóhomomorfizmus, kongruencia, ideál, filter, ultrafilter. A moduláris háló fogalma, példák. Birkhoff és Dedekind tételei. Szabad Abel-csoport és kommutatív egységelemes gyűrű.
14. alkalom. A három elemmel generált szabad moduláris háló szerkezete. Alkalmazás: Birkhoff tétele. A dimenziófüggvény és Neumann-féle koordinátázás moduláris hálókban, Pálfy Péter Pál és Szabó Csaba tétele (csak mese). Egy páros gráf által indukált Galois-kapcsolat. Példák: Galois-elmélet, a teljes mátrixgyűrű balideáljai. A fogalomanalízis elemei.